Comparison of magnetic diffusion and reconnection in ideal and resistive relativistic magnetohydrodynamics, ideal magnetodynamics and resistive force-free electrodynamics
Mar 25, 2025·, ,,,·
0 min read
,,,·
0 min read
Michael P. Grehan
Tanisha Ghosal
James R. Beattie
Bart Ripperda
Oliver Porth
Fabio Bacchini
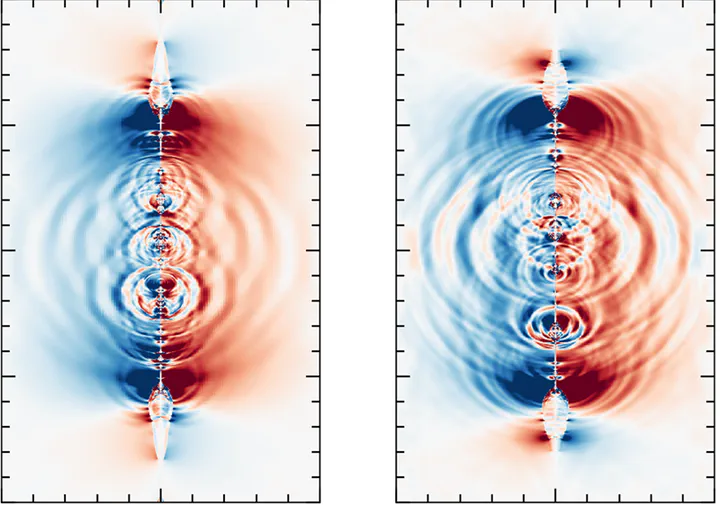 Fast magnetosonic waves radiating from nonlinear tearing instabilities developing in a reconnecting current sheet.
Fast magnetosonic waves radiating from nonlinear tearing instabilities developing in a reconnecting current sheet.Abstract
High-energy astrophysical systems and compact objects are frequently modeled using ideal relativistic magnetohydrodynamic (MHD) or force-free electrodynamic (FFE) simulations, with the underlying assumption that the discretisation from the numerical scheme introduces an effective (numerical) magnetic resistivity that adequately resembles an explicit resistivity. However, it is crucial to note that numerical resistivity can fail to replicate essential features of explicit resistivity. In this study, we compare the 1D resistive decay and 2D reconnection properties of four commonly used physical models. We demonstrate that the 1D Ohmic decay of current sheets via numerical dissipation in both ideal MHD and magnetodynamics (MD) is subdiffusive (i.e., sub-linear in time), whereas explicit resistive FFE and resistive MHD simulations match the predictions of resistive theory adequately. For low-resolution, reconnecting current sheets in 2D, we show that ideal MHD and MD have an analogue to the Sweet–Parker regime where the scaling of the reconnection rate depends directly on the resolution. At high resolutions, ideal MHD and MD have an asymptotic reconnection rate similar to resistive MHD. Furthermore, we find that guide field-balanced current sheets in ideal MHD and MD have a qualitative structure similar to that of one in resistive MHD. Similarly, a pressure-balanced current sheet in ideal MHD is found to have a qualitative structure similar to that of one in resistive MHD. For a guide field-balanced sheet, resistive FFE is found to have a nearly identical Sweet–Parker regime compared to resistive MHD and a similar asymptotic reconnection rate for large enough Lundquist numbers, but differs in the timescale for reconnection onset in the asymptotic regime. We discuss the implications of our findings for global simulations.
Type