Fundamental MHD scales -- II: the kinematic phase of the supersonic small-scale dynamo
Jan 31, 2025· ,,,·
0 min read
,,,·
0 min read
Neco Kriel
James R. Beattie
Christoph Federrath
Mark R. Krumholz
Justin Kin Jun Hew
 A new model for how the magnetic field spectrum changes during the kinematic stage of the small-scale dynamo.
A new model for how the magnetic field spectrum changes during the kinematic stage of the small-scale dynamo.Abstract
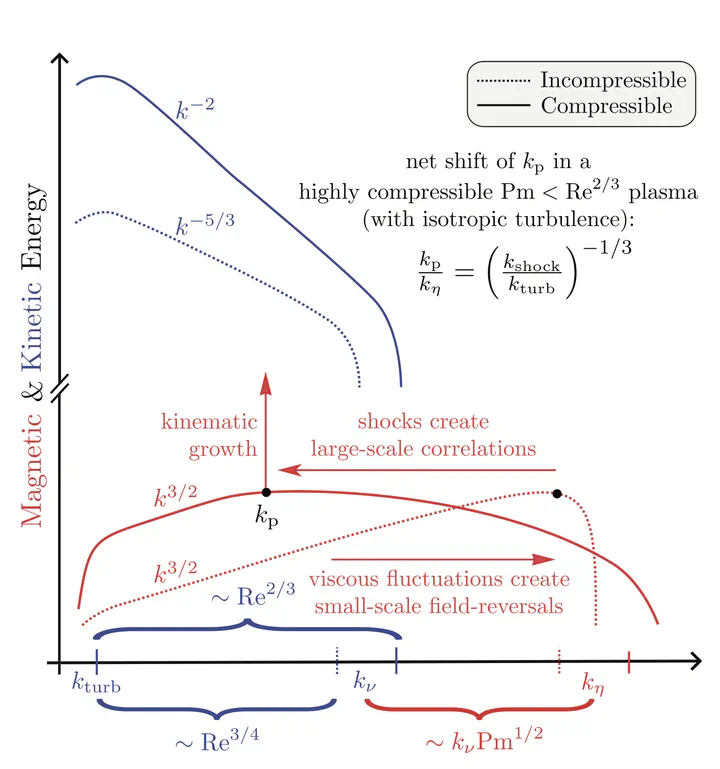
Many astrophysical small-scale dynamos (SSDs) amplify weak magnetic fields via highly compressible, supersonic turbulence, but most established SSD theories have only considered incompressible flows. To address this gap, we perform viscoresistive SSD simulations across a range of sonic Mach numbers ( M ), hydrodynamic Reynolds numbers ( Re ), and magnetic Prandtl numbers ( Pm ), focusing on the exponential growth phase. From these simulations, we develop robust measurements of the kinetic and magnetic energy dissipation scales ( ℓν and ℓη , respectively), and show that ℓν/ℓη∼Pm1/2 is a universal feature of turbulent ( Re≥Recrit≈100 ), Pm≥1 SSDs, regardless of M . We also measure the scale of maximum magnetic field strength ( ℓp ), where we confirm that incompressible SSDs (where either M≤1 or Re<Recrit ) concentrate magnetic energy at ℓp∼ℓη with inversely correlated field strength and curvature. By contrast, for compressible SSDs (where M>1 and Re≥Recrit ), shocks concentrate magnetic energy in large, overdense, coherent structures with ℓp∼(ℓturb/ℓshock)1/3ℓη≫ℓη , where ℓshock is the characteristic shock width, and ℓturb is the outer scale of the turbulent field. When Pm<Re2/3 , the shift of ℓp (from the incompressible to compressible flow regime) is large enough to move the peak magnetic energy scale out of the subviscous range, and the plasma converges on a hierarchy of scales – ℓturb>ℓp>ℓshock>ℓν>ℓη . In the compressible flow regime, more broadly, we also find that magnetic field-line curvature becomes nearly independent of the field strength, not because the field geometry has changed, but instead the field becomes locally amplified through flux-frozen compression by shocks. These results have implications for various astrophysical plasma environments in the early Universe, and cosmic ray transport models in the interstellar medium.
Type