Taking control of compressible modes: bulk viscosity and the turbulent dynamo

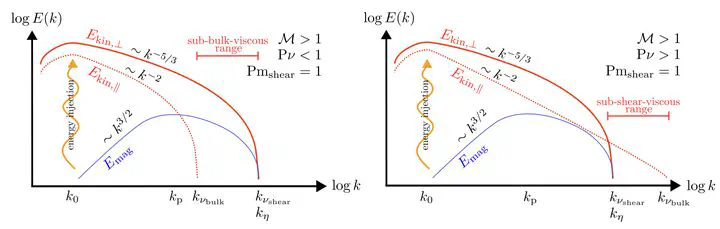
Many polyatomic astrophysical plasmas are compressible and out of chemical and thermal equilibrium, and yet, due to Stokes’ hypothesis, a means to carefully control the decay of compressible modes in these systems has largely been neglected. This is especially important for small-scale, turbulent dynamo processes, which are known to be sensitive to the effects of compression. To control the viscous properties of the compressible modes, we perform supersonic, visco-resistive dynamo simulations with additional bulk viscosity νbulk, deriving a new νbulk Reynolds number Rebulk, and viscous Prandtl number Pν≡Rebulk/Reshear, where Reshear is the shear viscosity Reynolds number. For 10−3≤Pν≤∞, we explore a broad range of statistics critical to the dynamo problem, including the integral and spectral energy ratios, growth rates, and the magnetic Emag(k) and kinetic Ekin(k) energy spectrum. We derive a general framework for decomposing Emag growth rates into incompressible and compressible terms via orthogonal tensor decompositions of ∇⊗v, where v is the fluid velocity. We find that compressible modes play a dual role, growing and decaying Emag, and that field-line stretching is the main driver of growth, even in supersonic dynamos. In the absence of νbulk, compressible modes pile up on small-scales, creating an apparent spectral bottleneck, which disappears for Pν≈1. As Pν decreases, compressible modes are dissipated at increasingly larger scales, in turn suppressing incompressible modes through a coupling between viscosity operators. We emphasise the importance of further understanding the role of νbulk in compressible astrophysical plasmas.